Siv3Dで振り子のシミュレーション
Siv3Dで振り子のシミュレーションを作ってみました
はじめに
つい先日、解析力学で振り子の運動についてちょろっと学んだのですが。
これシミュレーションしたら面白そうだなあと思ったので、OpenSiv3Dで作りました。
動機としてはこれだけです。
今回は単振り子と、ちょっと頑張って二重振り子の2つを実装します。
この実装のソースコードはこちらのGitHubページに。
単振り子シミュレーション
まずは単振り子のシミュレーションを作ります。
単振り子の運動方程式は以下のように与えられます。
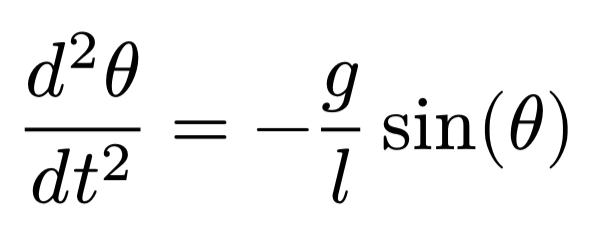
いつもの物理学なら、この微分方程式を解いて……とやりますが、今回はシミュレーションなので数値計算です。
つまり、この微分方程式から各加速度が求まれば、微小時間をかけて角速度に、さらにもう一回かけて角度にしていけばいいわけです。
これをOpenSiv3Dで実装します。
とりあえず、シミュレーションに必要なパラメータやメソッドをまとめたクラスを作ります。
/// @brief 単振り子のシミュレーション
class SimplePendulum {
protected:
const double g = 9.8; // 重力加速度
const double length0 = 1.0; // 振り子の長さ
double theta0 = 0.5_pi; // 角度の初期値
double theta0_v = 0.0; // 角速度
double theta0_a = 0.0; // 角加速度
Vec2 coordinate{ 0.0, 0.0 }; // 振り子のx,y座標
double scale = 1.0; // 振り子のスケール
Vec2 offset{ 0.0, 0.0 }; // 振り子のオフセット座標
public:
// 振り子パラメターの初期化
SimplePendulum(
double theta = 0.5_pi, double length = 1.0, double gravity = 9.8,
double scale = 1.0, Vec2 offset = Vec2{ 0.0, 0.0 }
);
// 振り子を更新
void update(void);
// 振り子のx,y座標を取得
Vec2 get_coordinate(void) const;
void set_scale(double scale);
double get_scale(void) const;
void set_offset(const Vec2& offset);
Vec2 get_offset(void) const;
};シミュレーションに必須のパラメーターとして以下の3つが挙げられます。
- 初期角度
- 振り子の長さ
- 重力加速度
角速度、角加速度もシミュレーションでは用いますが、初期条件としてどちらも0.0であるとしておきます。
また、振り子のx,y座標とスケール、オフセット座標は、シミュレーションの結果を見やすくするために用います。
そして、メソッドの実装です。
/// @brief 単振り子パラメータの初期化
/// @param theta 初期角度 (初期値: pi/2)
/// @param length 振り子の長さ (初期値: 1.0)
/// @param gravity 重力加速度 (初期値: 9.8)
SimplePendulum::SimplePendulum(
double theta, double length, double gravity,
double scale, Vec2 offset
) : theta0(theta), length0(length), g(gravity), scale(scale), offset(offset) {}
/// @brief 振り子を更新
/// @return 振り子のx,y座標
void SimplePendulum::update(void) {
this->theta0_a = -g * Sin(theta0) / length0;
this->theta0_v += theta0_a * Scene::DeltaTime();
this->theta0 += theta0_v * Scene::DeltaTime();
this->coordinate = Vec2{
length0 * Sin(theta0),
length0 * Cos(theta0)
};
}
Vec2 SimplePendulum::get_coordinate(void) const {
return this->coordinate * scale + offset;
}一部セッターゲッターのメソッドは省略しています。
運動方程式のとおり、角加速度の式を作成します。this->theta0_a = -g * Sin(theta0) / length0;
まず微小時間dtは、Scene::DeltaTime()(60fpsであれば基本的に約0.0167秒)を用います。
この微小時間を各加速度にかけて角速度、角速度にかけて角度を計算します。
そして、これをx,y座標に変換して、振り子の座標を更新します。座標を取得する際は、座標にスケールをかけてオフセットを足します。
こうしてできたものがこちらになります。
振り子の長さを変えたり、重力加速度を変えたり、初期角度を変えたりと、各種パラメータをいじったものです。
振り子らしい線分は省略していますが、それでもおおよそ大丈夫そうに見えます。
二重振り子シミュレーション
さて、次は二重振り子のシミュレーションを作ります。
二重振り子の運動方程式についてですが、流石に導出とかも面倒なので調べることにします。
こちらのQiita記事「Processingで二重振り子(Double Pendulum)の軌跡を描く」が参考になりそうです。
二重振り子のクラスも同様に作成しますが、パラメータやメソッドなど共通箇所が多いので、単振り子クラスを継承して作成します。
/// @brief 二重振り子のシミュレーション
class DoublePendulum : public SimplePendulum {
protected:
const double mass0 = 1.0; // 0番目の振り子の質量
const double mass1 = 1.0; // 1番目の振り子の質量
const double length1 = 1.0;
double theta1 = 0.5_pi;
double theta1_v = 0.0;
double theta1_a = 0.0;
Vec2 coordinate0{ 0.0, 0.0 };
Vec2 coordinate1{ 0.0, 0.0 };
public:
DoublePendulum(
double theta0 = 0.5_pi, double length0 = 1.0, double mass0 = 1.0,
double theta1 = 0.5_pi, double length1 = 1.0, double mass1 = 1.0,
double gravity = 9.8,
double scale = 1.0, Vec2 off_set = Vec2{ 0.0, 0.0 }
);
// 振り子を更新
void update(void);
// 0番目の振り子のx,y座標を取得
Vec2 get_coordinate0(void) const;
// 1番目の振り子のx,y座標を取得
Vec2 get_coordinate1(void) const;
};大きな違いといえば、振り子の質量が必要になったことでしょうか。
単振り子であれば、運動方程式の導出過程で質量変数がきれいに消えますが、二重振り子ではそうはいかないですからね。
また二重振り子では、0番目の振り子の座標を取得するメソッドと、1番目の振り子の座標を取得するメソッドを作成しておきます。
そして、メソッドの実装です。
/// @brief 二重振り子のパラメータの初期値
/// @param theta0 0番目の振り子の初期角度 (初期値: pi/2)
/// @param length0 0番目の振り子の長さ (初期値: 1.0)
/// @param theta1 1番目の振り子の初期角度 (初期値: pi/2)
/// @param length1 1番目の振り子の長さ (初期値: 1.0)
/// @param gravity 重力加速度 (初期値: 9.8)
DoublePendulum::DoublePendulum(
double theta0, double length0, double mass0,
double theta1, double length1, double mass1,
double gravity,
double scale, Vec2 off_set
): SimplePendulum(theta0, length0, gravity, scale, off_set), mass0(mass0), theta1(theta1), length1(length1), mass1(mass1) {}
void DoublePendulum::update(void) {
double delta_time = Scene::DeltaTime();
theta0_a = (-g * (2 * mass0 + mass1) * Sin(theta0) - mass1 * g * Sin(theta0 - theta1) - 2 * Sin(theta0 - theta1) * mass1 * (Pow(theta1_v, 2) * length1 + Pow(theta0_v, 2) * length0 * Cos(theta0 - theta1))) / (length0 * (2 * mass0 + mass1 - mass1 * Cos(2 * theta0 - 2 * theta1)));
theta1_a = (2 * Sin(theta0 - theta1) * (Pow(theta0_v, 2) * length0 * (mass0 + mass1) + g * (mass0 + mass1) * Cos(theta0) + Pow(theta1_v, 2) * length1 * mass1 * Cos(theta0 - theta1))) / (length1 * (2 * mass0 + mass1 - mass1 * Cos(2 * theta0 - 2 * theta1)));
theta0_v += theta0_a * delta_time;
theta1_v += theta1_a * delta_time;
theta0 += theta0_v * delta_time;
theta1 += theta1_v * delta_time;
this->coordinate0 = Vec2{
length0 * Sin(theta0),
length0 * Cos(theta0)
};
this->coordinate1 = Vec2{
length0 * Sin(theta0) + length1 * Sin(theta1),
length0 * Cos(theta0) + length1 * Cos(theta1)
};
}
Vec2 DoublePendulum::get_coordinate0(void)const {
return this->coordinate0 * scale + offset;
}
Vec2 DoublePendulum::get_coordinate1(void)const {
return this->coordinate1 * scale + offset;
} 単振り子クラスのコンストラクタを使用して、変数の初期化を楽しちゃいましょう。
あとは運動方程式を頑張って実装します。丸括弧のズレに注意。
そうして角加速度を出せたら、単振り子のときと同じように角速度、角度、x,y座標を更新します。
早速シミュレーションを行ってみましょう。
単振り子よりも複雑な軌跡を描くので、過去の軌跡を残すようにしました。
いかにも二重振り子ってかんじが出てきました。先端の振り子がくるくる回るのとか、かなりそれっぽい。
せっかく二重振り子を作ったので、カオス性についても確認したいですよね。
初期角度を0.500000πと0.499999πにし、それ以外のパラメータを全く同じものにした2つの二重振り子で比較してみます。
その差わずか0.000001π。これでも軌跡に違いは出るのでしょうか。
開始数秒はどちらも同じように見えますが、その後徐々に軌跡がずれ始め、最終的には全く異なる動きをし始めました。
おわりに
今回は二重振り子のシミュレーションを作成しました。
かなり突貫気味な実装でしたが、それでもカオス性がしっかり表れていて、個人としては大満足です。
せっかく作ったので何かに活かせるといいなあ、と思っています。まだ何もアイデアはないですが。